Entropy, Free energy principle, Maximum entropy principle, Desmos graph calculator
Calculus
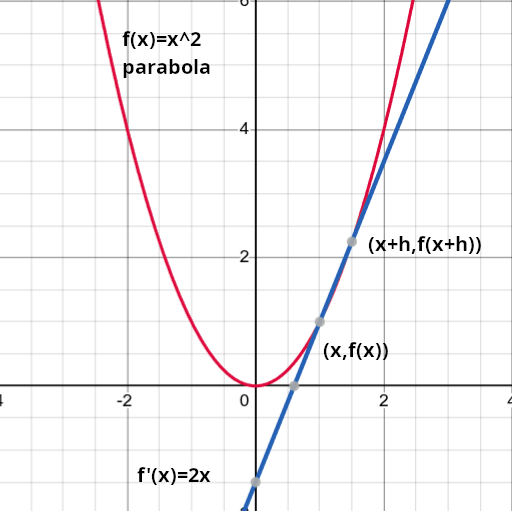
Understanding {$f'(x)=\lim_{h\rightarrow 0}\frac {f(x+h)-f(x)}{h}$}
{$f'(x)$} is the derivative of {$f(x)$} at {$x$}
We can write {$f'(x_0)=\lim_{x\rightarrow x_0}\frac {f(x_0)-f(x)}{x_0-x}$} which makes clear that a derivative is the limit of a slope.
If we set {$x_0=x+h$} then note that {$x_0-x=(x+h)-x=h$}. We get {$f'(x)=\lim_{h\rightarrow 0}\frac {f(x+h)-f(x)}{h}$} which makes clear that a derivative results from a tiny perturbation {$h$} of the value {$x$}. We are comparing {$f(x)$} and {$f(x+h)$} in terms of {$h$}. This form is convenient for the calculations below.
Focus on the case when {$f(x)$} is a polynomial
Consider the cases {$f(x)=1, f(x)=x, f(x)=x^2, f(x)=x^3\dots $}
{$f(x)=1$}
{$f'(x)=\lim_{h\rightarrow 0}\frac {f(x+h)-f(x)}{h}=\lim_{h\rightarrow 0}\frac {1-1}{h}=\lim_{h\rightarrow 0}\frac{0}{h}=\lim_{h\rightarrow 0}0=0$}
{$f'(x)=0$}
Multiply by a constant: {$g(x)=Cf(x)$}
{$g'(x)=\lim_{h\rightarrow 0}\frac {g(x+h)-g(x)}{h}=\lim_{h\rightarrow 0}\frac {Cf(x+h)-Cf(x)}{h}=\lim_{h\rightarrow 0}C\frac{f(x+h)-f(x)}{h}=C\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}=Cf'(x)$}
{$g(x)=C$}
{$g(x)=C\cdot 1$}
{$g(x)=C f(x)$} where {$f(x)=1$}
{$g'(x)=C f'(x)=C\cdot 0 = 0$}
{$f(x)=x$}
{$f'(x)=\lim_{h\rightarrow 0}\frac {f(x+h)-f(x)}{h}=\lim_{h\rightarrow 0}\frac {x+h-x}{h}=\lim_{h\rightarrow 0}\frac {h}{h}=\lim_{h\rightarrow 0}1=1$}
{$f'(x)=1$}
{$f(x)=Cx$}
{$f'(x)=C\cdot 1$}
{$f'(x)=C$}
{$f(x)=A(x)+B(x)$}
{$f'(x)=\lim_{h\rightarrow 0}\frac {f(x+h)-f(x)}{h}=\lim_{h\rightarrow 0}\frac {A(x+h)+B(x+h)-A(x)-B(x)}{h}=\lim_{h\rightarrow 0}\frac {A(x+h)-A(x)+B(x+h)-B(x)}{h}$}
{$=\lim_{h\rightarrow 0}\frac {A(x+h)-A(x)}{h}+\lim_{h\rightarrow 0}\frac {B(x+h)-B(x)}{h}= A'(x)+B'(x)$}
{$f'(x)=A'(x)+B'(x)$}
{$f(x)=mx+b$} Line with slope {$m$} and y-intercept {$b$}
{$f'(x)=(mx)' + (b)'$}
{$f'(x)=m + 0 = m$}
| {$f'(x)=m$} | The derivative of a line is its slope. |
{$f(x)=x^2$}
{$f'(x)=\lim_{h\rightarrow 0}\frac {f(x+h)-f(x)}{h}=\lim_{h\rightarrow 0}\frac {(x+h)^2-x^2}{h}=\lim_{h\rightarrow 0}\frac {(x+h)(x+h)-x^2}{h}=\lim_{h\rightarrow 0}\frac {x^2+xh+hx+h^2-x^2}{h}$}
{$=\lim_{h\rightarrow 0}\frac {x^2+2xh+h^2-x^2}{h}=\lim_{h\rightarrow 0}\frac {2xh+h^2}{h}=\lim_{h\rightarrow 0} 2x + h=2x$}
{$f'(x)=2x$}
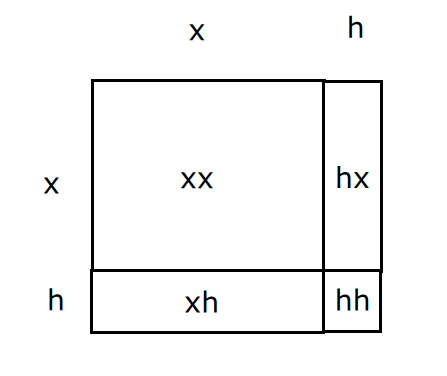
{$(x+h)(x+h)=xx + xh + hx + hh$}
An example of the limiting process
| {$\mathbf{f(x)=x^2}$} | {$\mathbf{f'(x)=2x}$} | {$\mathbf{f'(1)=2}$} |
| {$\mathbf{x}$} | {$\mathbf{h}$} | {$\mathbf{x+h}$} | {$\mathbf{f(x)}$} | {$\mathbf{f(x+h)}$} | {$\mathbf{f(x+h)-f(x)}$} | {$\mathbf{\frac{f(x+h)-f(x)}{h}}$} |
| {$1$} | {$1$} | {$2$} | {$1$} | {$4$} | {$3$} | {$3$} |
| {$1$} | {$.1$} | {$1.1$} | {$1$} | {$1.21$} | {$.21$} | {$2.1$} |
| {$1$} | {$.01$} | {$1.01$} | {$1$} | {$1.0201$} | {$.0201$} | {$2.01$} |
| {$1$} | {$.001$} | {$1.001$} | {$1$} | {$1.002001$} | {$.002001$} | {$2.001$} |
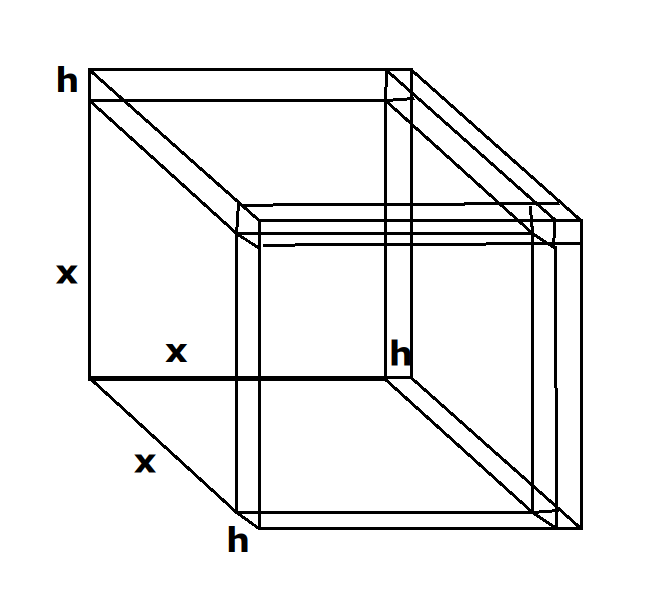
{$(x+h)^3=xxx + xxh + xhx + hxx + xhh + hxh + hhx + hhh$}
{$f(x)=x^3$}
{$f'(x)=\lim_{h\rightarrow 0}\frac {f(x+h)-f(x)}{h}$}
{$f'(x)=\lim_{h\rightarrow 0}\frac {f(x+h)-f(x)}{h}=\lim_{h\rightarrow 0}\frac {(x+h)^3-x^3}{h}=\lim_{h\rightarrow 0}\frac {(x+h)(x+h)-x^3}{h}=\lim_{h\rightarrow 0}\frac {xxx+xxh+xhx+hxx+xhh+hxh+hhx+hhh - xxx}{h}$}
{$=\lim_{h\rightarrow 0}\frac {x^3+3x^2h+3xh^2+h^3-x^3}{h}=\lim_{h\rightarrow 0}\frac {3x^2h+2xh^2+h^3}{h}=\lim_{h\rightarrow 0} 3x^2+3xh+h^2=3x^2$}
{$f'(x)=3x^2$}
| {$\mathbf{(x+h)^n}$} |
| {$1$} | |||||||||||||||||||||
| {$x$} | {$h$} | ||||||||||||||||||||
| {$x^2$} | {$2xh$} | {$h^2$} | |||||||||||||||||||
| {$x^3$} | {$3x^2h$} | {$3xh^2$} | {$h^3$} | ||||||||||||||||||
| {$x^4$} | {$4x^3h$} | {$6x^2h^2$} | {$4xh^3$} | {$h^4$} | |||||||||||||||||
| {$x^5$} | {$5x^4h$} | {$10x^3h^2$} | {$10x^2h^3$} | {$5xh^4$} | {$h^5$} | ||||||||||||||||
| {$x^6$} | {$6x^5h$} | {$15x^4h^2$} | {$20x^3h^3$} | {$15x^2h^4$} | {$6xh^5$} | {$h^6$} | |||||||||||||||
| {$x^7$} | {$7x^6h$} | {$21x^5h^2$} | {$35x^4h^3$} | {$35x^3h^4$} | {$21x^2h^5$} | {$7xh^6$} | {$h^7$} | ||||||||||||||
| {$x^8$} | {$8x^7h$} | {$28x^6h^2$} | {$56x^5h^3$} | {$70x^4h^4$} | {$56x^3h^5$} | {$28x^2h^6$} | {$8xh^7$} | {$h^8$} | |||||||||||||
| {$x^9$} | {$9x^8h$} | {$36x^7h^2$} | {$84x^6h^3$} | {$126x^5h^4$} | {$126x^4h^5$} | {$84x^3h^6$} | {$36x^2h^7$} | {$9xh^8$} | {$h^9$} | ||||||||||||
| {$x^{10}$} | {$10x^9h$} | {$45x^8h^2$} | {$120x^7h^3$} | {$210x^6h^4$} | {$252x^5h^5$} | {$210x^4h^6$} | {$120x^3h^7$} | {$45x^2h^8$} | {$10xh^9$} | {$h^{10}$} |
{$\binom{n}{k}=\frac{n!}{k!(n-k)!}$}
Proof of luck = Proof of work = Uncovering 0 or 1
| 0 | 1 | |||||||
| 00 | 01 10 | 11 | ||||||
| 000 | 001 010 100 | 011 101 110 | 111 | |||||
| 0000 | 0001 0010 0100 1000 | 0011 0101 0110 1001 1010 1100 | 0111 1011 1101 1110 | 1111 |
Compare with alphabetical order (which I think is the same pas Proof of Entropy Minima)
| 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |