Qi Quai Report
by Andrius Kulikauskas for Steph Macurdy
December 3, 2025
Contents
- Introduction and Summary
- Evaluating the Qi Quai System
- Critical Facts
- Marketing
- Overcomplicating and underexplaining
- Values and priorities
- Understanding the Qi Quai protocol
- Reward mechanism for receiving Qi or Quai
- Updating {$k_{Qi}$}
- Updating {$k_{Quai}$}
- Investigating the Future of Dual Currency Systems
- The merit of two or three currencies
- The economics of maintenance
- The cost of doing business
- Thermodynamics: Energy, entropy, free energy
Introduction and Summary
The Qi Quai cryptocurrency system, in its documentation, highlights the concepts of energy and entropy. In thermodynamics, these concepts are linked by free energy, which suggests the possible relevance of Karl Friston's Free Energy Principle by which the brain and other such predictive systems minimize surprise. The Free Energy Principle is central to the Active Inference theoretical framework, which models an agent's relationship with its environment. Notably, in a perception-action loop, when a prediction is incorrect, then the agent may update its model or the world. This branching of possibilities is attractive in that it honors conflicting perspectives by which our will is consequential (we may update the model or the world) but our fate is inevitable (it is governed by the minimization of free energy). Mathematically, the equations juxtapose various factors such as exploration vs. exploitation, complexity vs. accuracy, divergence vs. evidence and ambiguity vs. risk.
Can Active Inference or any other theoretical framework offer insight into the relationship between Qi and Quai?
Steph, this is my summary for you of my findings from my work for you and with you in September, October, November 2025.
In the big picture, most optimistically, Qi and Quai are the foundations of a new global economy, independent of national fiat currencies, reserve systems and power structures. As a dual currency system, they are solving the problem of a typical cryptocurrency, such as Bitcoin, which are all priced in dollars, which is to say, the existing system. Instead, Quai would be priced in Qi, as would everything else.
The principle underlying this is the disentangling of the functions of money, reviving bimetallism (as when gold and silver currencies coexist), and driven by Gresham's law, whereby "bad money chases out good". The "bad money" is exchanged and the "good money" is hoarded. Qi is the intended unit of exchange and Quai is the intended storage of value. Here Gresham's law functions as a feature and not a bug.
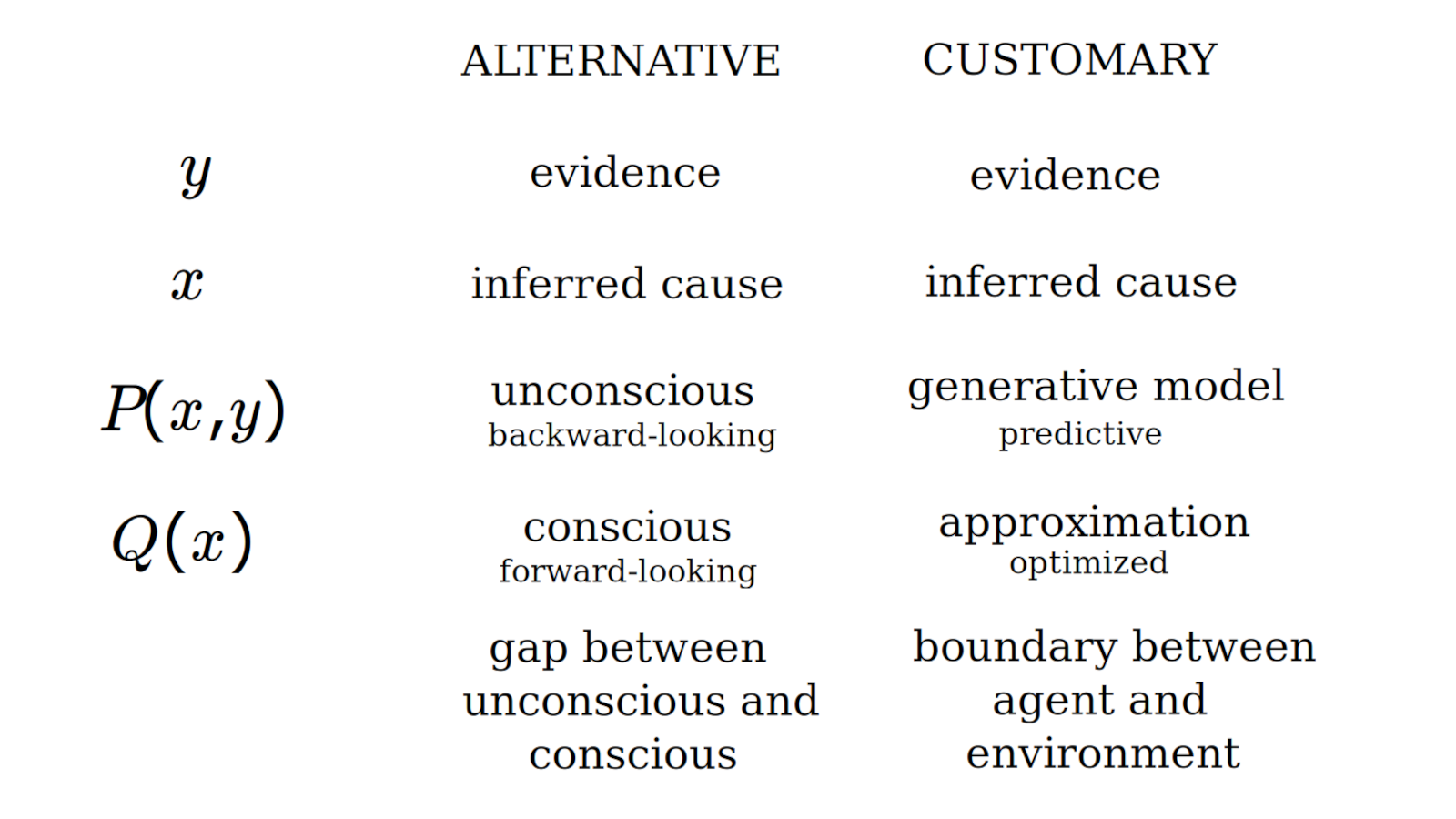
Conceptually, we seek a theoretical framework, an analogy that would help us think through the relationship between Qi and Quai. Specifically, we are constructing a bridge between cryptocurrency and thermodynamics. We proceed from both directions. Starting with cryptocurrency, we consider the relationship between Qi and Quai in recent history, as implemented in the protocol, and in terms of behavioral incentives. Starting with thermodynamics, we analyze the equation by which energy is divided into free energy and entropy, representing useful work and useless work. This equation relates two probability distributions P(x,y) and Q(x). Mathematically, we interpret P(x,y) and Q(x) from the customary Active Inference perspective, where Q(x) approximates P(x|y) optimally, and also from an alternative perspective, where Q(x) and P(x,y) are in dialogue. Our ultimate goal is to understand the Qi Quai protocol in terms of a control mechanism, such as a Kalman filter, whose behavior we might be able to relate to the concepts of energy, entropy and free energy.
I was able to map out how the protocol updates the key parameter {$k_{Quai}$} and to distill that to an algorithm of the form {$k_{Quai}(i)=k_{Quai}(i-1)[1\pm r]$} where the plus-or-minus sign is determined by the voting system which indicates whether participants prefer Qi over Quai, in which case the plus sign holds and {$k_{Quai}$} is increased, or whether they prefer Quai over Qi, in which case the minus sign holds and {$k_{Quai}$} is decreased. Basically, this means that the evolution of {$k_{Quai}$} depends on the actual preferences.
At this point, we want some kind of empirical evidence about those preferences. Otherwise, we are building theories out of thin air. The protocol's control mechanism supposes that to balance Qi and Quai, it is enough to increase {$k_{Quai}$} when there is a preference for Qi and reduce it when there is a preference for Quai. However, if we take an economic or game theory perspective, and consider rational behavior, then miners will choose to mine when difficulty is abnormally low, and will refrain from mining when difficulty is abnormally high, regardless of the value of {$k_{Quai}$}, for difficulty increases exponentially but rewards do not. This is a subtle question that requires empirical evidence to examine it in a real life context.
As regards Active Inference, my analysis of the equation relating energy, entropy and free energy shows that it stands independently of the many assumptions of the Active Inference framework. Under the customary interpretation, {$Q(x)$} approximates {$P(x|y)$}, and we can think of the probability {$P(x,y)$} of both {$x$} and {$y$} as being compressed to yield the probability {$P(x|y)$} of {$x$} given {$y$}. Instead, I propose an alternative interpretation of a dialogue between two levels of awareness, a sensory {$P(x,y)$} with access to evidence {$y$} and a conceptual {$Q(x)$} without access to this evidence. These can be understood as Kahneman and Tversky's fast-thinking System 1 and slow-thinking System 2, respectively, and there are hundreds of other examples at Theory Translator.
This alternative interpretation can be the starting point of an exploration of thermodynamic foundations for a two currency economic system. Thus I interpret in some detail the equation for energy (as free energy and entropy) and another equation for free energy (as divergence and knowledge gained).
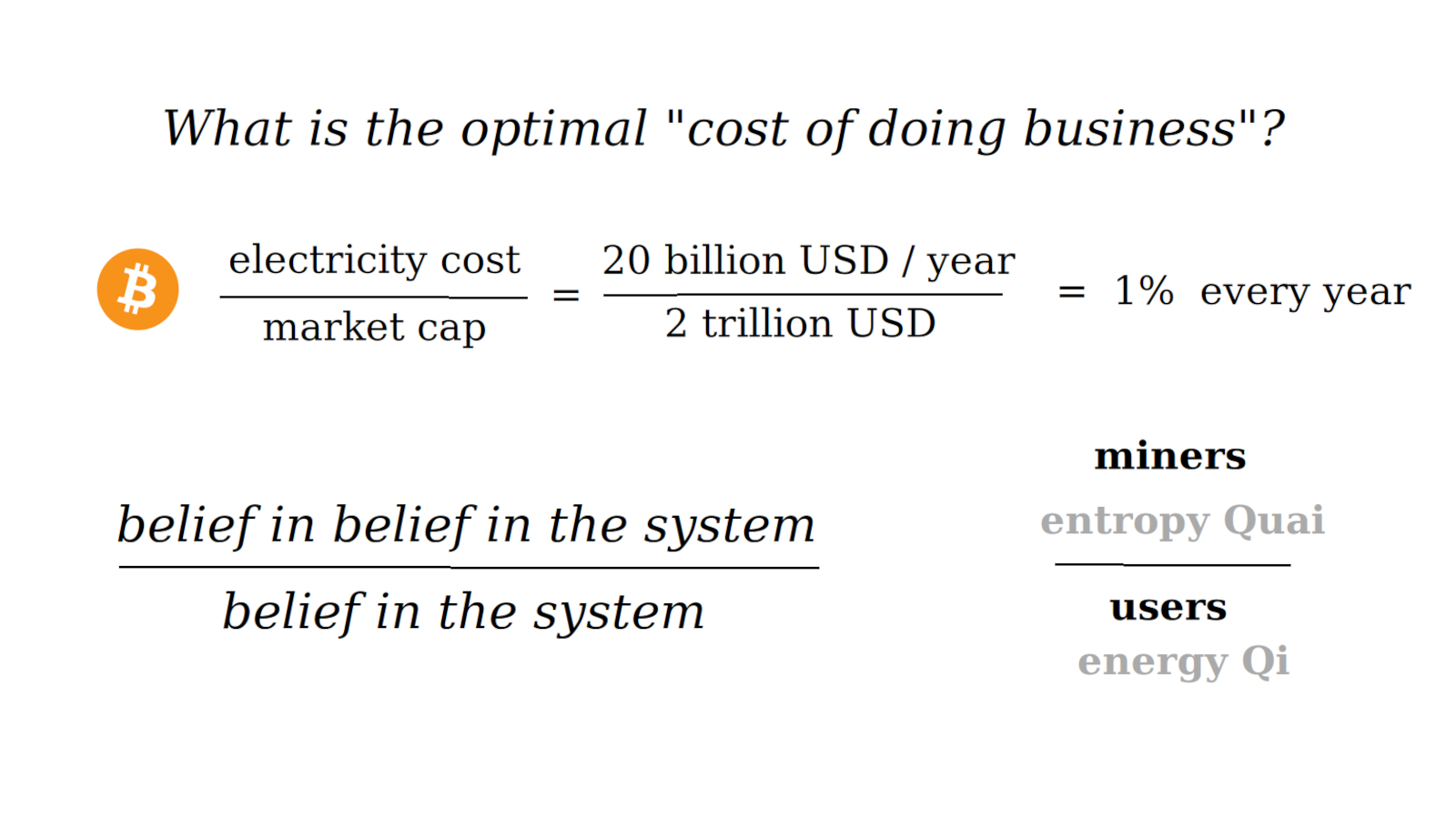
Empirically, a key relationship to explore is the ratio between mining costs and market capitalization. In the case of Bitcoin, this ratio has indicated when the currency has been undervalued. This indicator may be relevant for an economics of maintenance.
Conceptually, the concept of "the cost of doing business", as applied to a civilization or an economy, seems to be helpful. By this I mean not the total costs but rather the minimal ongoing costs to keep a system running. For a typical cryptocurrency system, this is the cost of mining, the "proof of work" which is inherently wasteful. It is meaningful to compare this to the costs that our current economic system depends on, which include an ever expanding financial industry, a military industrial complex, a reserve system that legislates exponential growth, and when that does not happen naturally, a moral caste system that ranks everybody by their credit rating, isolating, disparaging, abandoning and punishing accordingly, so that everybody has somebody to look down upon.
The distinction of levels of awareness can be understood as a distinction between "belief in a system" and "belief in belief in a system". When a new economic system is getting off the ground, there is nothing to believe in, and yet there are those organizers and investors who believe in that belief, which is to say, who believe that the system will become functional. The current Qi and Quai system attracts miners and hoarders even though, as of yet, there are no economic transactions to speak of. At a certain point, there will be miners who no longer believe in that belief, but who will be left with currency. That currency will be worth something to the remaining miners and may also be employed for transactions. Thus the success of the economic system will depend on those who believe in the system itself, and make use of it in their personal affairs, but do not believe in the belief of the system, and so do not invest themselves in it to enrich themselves. The latter is the "cost of doing business" for the economic system. Here we can imagine the roles that Qi for exchangers and Quai for hoarders may fulfill, and their relationships to free energy and entropy, respectively.
We can look at "the cost of doing business" in two ways. For a civilization, it means all of the essential activities that must be supported so that it does not collapse. Those activities are the intrinsic "entropy" of the civilization and, above and beyond that economy, there are the opportunities that arise from pooling resources, namely capitalistic projects, which express the "free energy" of the system. Yet alternatively, for that economy, the cost of doing business can be understood as all of the investment that its organizers need to make and be rewarded for, which is the intrinsic entropy. This economic system opens up a myriad of possibilities, the free energy, whereby individuals can decide for themselves how best to satisfy their economic needs and even desires. The fact that "the cost of doing business" can be understood in opposite ways, for a civilization and for its economy, may be a key point to master.
Evaluating the Qi Quai System
In evaluating the Qi Quai system, there are simple facts which may be more to the point than sophisticated theoretical analyses.
Most importantly, there is only a tiny chance that the Qi Quai system will grow to become a leading cryptocurrency, let alone the world's economic system. The reason is that even a perfectly well-founded system has little chance of success because luck is essential. An oak tree brings forth thousands of acorns but only a few of them take root. Similarly, the success of a cryptocurrency or any product depends on the peculiarities of its context, whether it is not too early and not too late, not underfunded and not overfunded, how it is branded and received, how it gets used or misused, how its stakeholders behave, how regulators and competitors respond, how the economy, technology and society evolve. Furthermore, there is no guarantee that one is crafting a well-founded system.
Another limitation to keep in mind is that the protocol for a system is fixed upon initiation. In theory, forks are possible, but in practice, the main fork is not ammended. This is a consequence of the requirement that the system be distributed with no central authority. Evidently, this constraint has worked well enough for Bitcoin and other major cryptocurrencies. We find a rather similar immutability with marital vows, religious scriptures and national constitutions. As participants invest in such a system, it may persist as a self-fulfilling prophecy. And yet it can be argued that such a system is less adaptive and less competitive than one which reflects and serves a community which has the power to modify it.
Critical Facts
As things stand, the Qi Quai system is not a real economy. It is not being used for real transactions, that is, for goods or services. This can be checked by inspecting the blocks. The only transactions are coinbase transactions, which is to say, the rewards that miners get for creating the coins.
The Qi Quai system has attracted a significant amount of money. On October 17, 2025, there was a total of 3 billion Quai, valued at $120,000,000, of which 617 million were circulating, valued at $25,000,000. There was a total of 130 thousand Qi, valued at $117,000. The numbers show, however, that this is a single currency system. The number of Quai to Qi in circulation is 5,000 to 1.
From this point of view, it is Qi that is scarce compared to Quai. Whereas Quai is supposed to be scarce compared to Qi. Note that today, in dollar terms, as given by the conversion dashboard, the value of Qi is $0.71 and the value of Quai is $0.03. By the logic of two currencies, miners should be mining and preferring the scarcer currency, but that is not the case.
By my calculation, for the current block number {$N=5,014,527$}, since the doubling period in blocks is {$D=16,966,368$} we have the technology adjustment factor {$T=1+\frac{N}{D}=1.3$}. The block difficulty is roughly {$d=755,000,000,000$}. The base {$b= 1/(8\times 10^9)$}. The Qi reward is {$b \times T \times d \approx 123 \textrm{ Qit}$} which is approximately {$87\times 0.001=$0.087$}. Whereas the Quai reward is given by {$k_{quai}\log_2 d=0.066\times 39.5 = 2.61 \textrm{ Quai}$} which is approximately $0.08. The two rewards are similar which suggests that the controller is working.
Here I note that when I originally queried the AI system quAI it calculated the Qi reward as 0.073 Qi. I challenged quAI because my answer was about 1,000 greater, and then it confirmed that my calculation was correct. But now I have understood that the reward is given in qits rather than qi, and that 1 qi = 1,000 qits. Note that nowhere are qits mentioned in the conversion documentation.
Miners are told that Quai is the scarce currency which will grow markedly in value. That is what they believe and what they act upon. Curiously, the organizers aren't encouraging the miners to mine both currencies. It's not clear why miners are choosing Quai or Qi rather than paying them with a basket of both currencies, which would make for a simpler, clearer, more predictable system, more in line with its intent. It's not clear why there needs to be a voting mechanism or why the conversions can't simply be handled by the market.
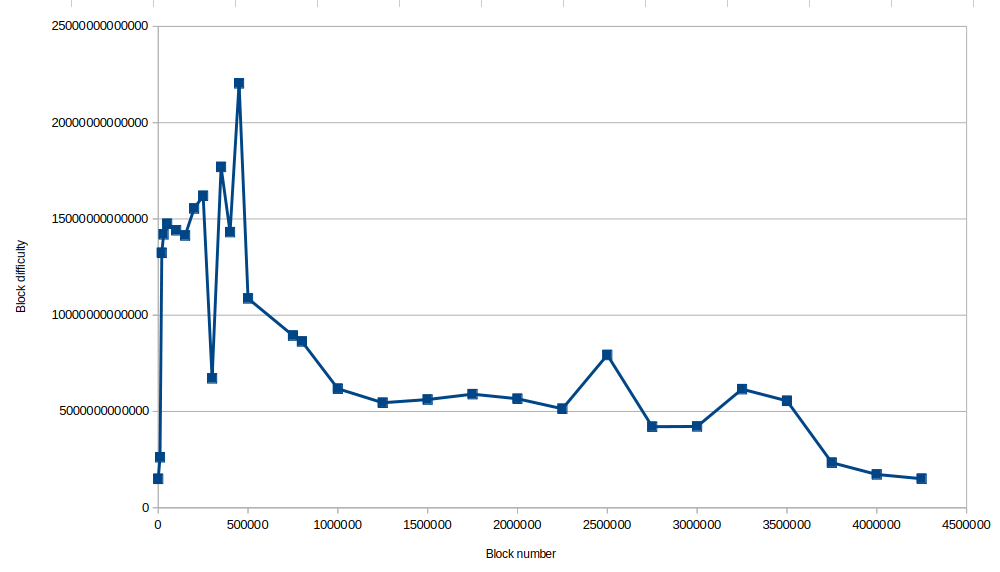
The block difficulty has been steadily decreasing, as shown by the graph below. This means that the popularity of the system has been steadily going down.
Historical data on the value of Qi and Quai is key to investigating the dynamics of their relationship. Any deeper theoretical analysis should make good use of it. This dual currency system is original and thus difficult to meaningfully compare with any other.
Marketing
The marketing of Qi and Quai is an important source of information for understanding the vision of the system and how profoundly or superficially it is implemented.
The Quai Network website is geared towards miners and developers. It presents Qi as the first decentralized energy dollar and notes that it is "Created proportionally to network mining hashrate and power requirements, positioning $QI as a true energy-based currency." The name Qi is based on the Chinese word which means "vital force". The documentation refers to the Energy-based currency as one of the system's three breakthrough innovations, the others being Proof-of-Entropy-Minima (for resolving conflicts among newly created blocks), and Merged-mined hierarchy (for organizing different levels of a hierarchy of networks). Overall, the marketing can have one think that energy and entropy are fundamental concepts on which this system is grounded.
How deeply is the vision followed through on? There does seem to be a purposefulness in designing this dual currency system so that Qi serves as means of exchange, reflecting the global cost of energy, and Quai serves as a store of value. This is reflected in the fact that Qi is emitted proportional to block difficulty whereas Quai is emitted proportional to the logarithm of block difficulty. However, that is as far and as deep as the logic seems to go. There is no theoretical framework that relates and clarifies these concepts of energy and entropy. There are no simulations that demonstrate the desired relationship. There is no white paper that provides an overall view of the science and engineering.
Instead, there are some superficial references to these concepts. Notably, "proof of entropy minimization" is a marketing term for what could otherwise be called "alphabetical order". The term does not shed light on the role that entropy plays here.
The term "proof of work" is historical but can be confusing here. It originally referred to the requirement that clients solve a puzzle to show that their requests are genuine and that they will pay a cost to receive the service they request from the server. Thus "work" here means "pointless efforts expended" rather than "useful efforts". An alternative way to express this would be to say that the client has "skin in the game".
In the protocol, a curious use of language is the application of the "discounts". From the miners' point of view, these are penalties. This is a twisting of words that seems designed to confuse.
Similarly, Qi could have been designed and described as "tied to the cost of computation". Instead, the emission of Qi depends on a technology factor that supposes that the cost of computation will halve every 2.69 years. This factor is only included for two doubling periods. After 5 years, the technology factor no longer changes. If the Qi Quai system is successful, then it will last much longer than 5 years. The point here is that using "the cost of computation" as a proxy for "the cost of energy" may be just a superficial marketing gesture. This could be criticized as "greenwashing".
The Qi Quai system is designed for a global economy but two design choices seem to be marketing choices geared for an American market. The denominations seem chosen to reflect the idiosyncratic US system of bills: 1 Qi, 5 Qi, 10 Qi, 20 Qi but no 50 Qi bill. The Chinese word 块 is spelled Kuai in Chinese Pinyin and spelling it Quai seems to be an Americanism. Both choices seem strange for a system which intends to replace the US dollar with an authentically global currency.
Overcomplicating and Underexplaining
The Qi Quai protocol can be criticized for overcomplicating some choices and underexplaining them.
Thus the emission of Quai is given by {$k_{Quai}$} times the logarithm (base 2) of the block difficulty. But what does this mean in practice? The block difficulty reached a maximum of roughly 14.7 trillion, for which the logarithm is 43.7, and is now at a minimum of roughly 0.7 trillion, for which the logarithm is 39.5. Thus the block difficulty dropped by 20 times but the logarithm dropped only 10 percent! The point is that when the block difficulty is such a large number, then from the logarithm's point of view, it is practically constant. For the logarithm to double from 40 to 80, the block difficulty would have to jump from a trillion to a trillion trillion. In that case, why have the logarithm at all? Practically speaking, it adds nothing in functionality but makes for pointless conceptual confusion.
In discussing the mechanics of the protocol, I will point out several constants that were added to tweak the calculations. Why those particular constants were added is unexplained. I presume that they were chosen because of numerical simulations that were performed. In that case, it would be meaningful to make those simulations available along with explanations.
In general, it seems that the system could have been simpler and thus better grounded in real principles.
Values and Principles
A very positive aspect of the Qi Quai community is its open nature. The protocol and code are open source. There is an active Discord community and there are many regular meetings where Karl Kreder and his team share news and answer questions. The AI bot quAI has proved very helpful in making sense of the intricate protocol.
On October 15, I attended a meeting where Karl Kreder answered my rather challenging questions. He agreed that there was an error in the Transaction Processing and Adjusted Difficulty section of the Conversions page in the documentation. The two choices given are logically the same choice, which is a problem. This error has been noted and will be fixed.
I asked about a comment in the protocol regarding the decrease in kQuai when Qi is preferred. He ultimately said that the comment was wrong. But I don't think it has ever been changed. And in fact, the comment is correct, as stated. It is the desired functionality that may be wrong, as I discuss later.
The conversions page, though rather detailed, is yet not completely clear. For example, the same {$alpha$} is used to mean two different parameters.
My general impression is that the functionality of the controller, and thus of the fundamentals of the two currency system, is a low priority.
There is no explanation how to know if the system is functioning properly. There is no simulation to show how the system could be working properly. There is no explanation of the assumptions for the underlying game theory, how participants are presumed to behave in various circumstances. There is no testbed for understanding if this economy can and should work. And there is no apparent demand for that from the participants, although the lack of assurance may make for a lack of demand.
Understanding the Qi Quai protocol
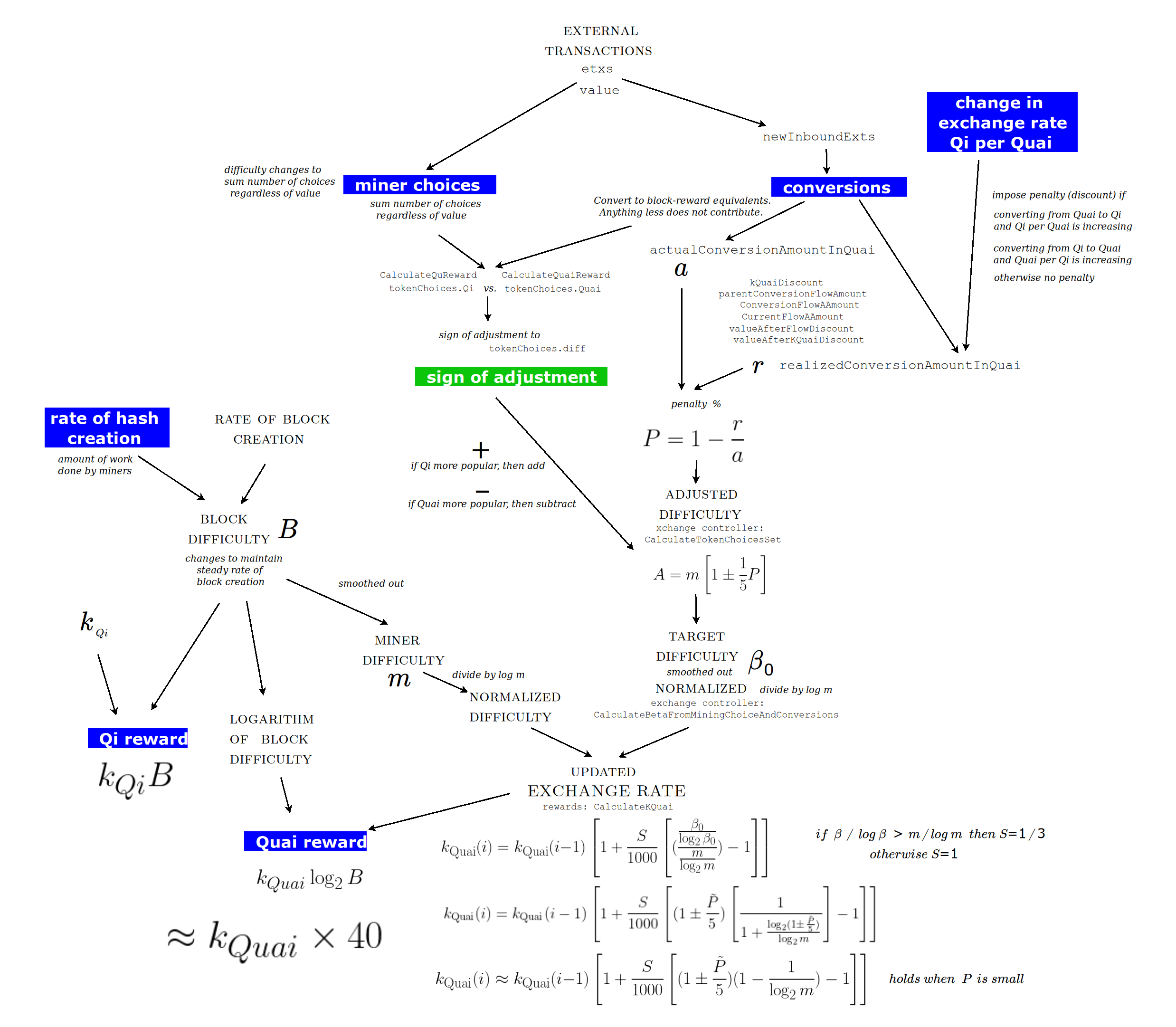
The relationship between Qi and Quai is the heart of the Qi Quai cryptocurrency system. Miners can choose to be rewarded in Qi or Quai. Furthermore, Qi can be converted into Quai and vice versa. The mechanisms are explained in the documentation and implemented in the protocol, which is written in the programming language Go, also known as Golang. The details are important in trying to understand the logic by which the price of Quai in terms of Qi can be expected to evolve. In the diagram above, I have summarized the essential points. I then distill them further to what is absolutely relevant.
We want to calculate the reward in Qi, which is straightforward, and the reward in Quai, which is more complicated, and which depends on a voting mechanism which determines whether Qi or Quai is more popular. But first let's locate in the protocol where the reward is given in Qi or Quai.
Reward mechanism for receiving Qi or Quai
Miners can choose to receive their reward in Qi or in Quai. The rewards depend on the block difficulty as well as the multipliers {$k_{Qi}$} and {$k_{Quai}$}. A crucial difference is that the reward in Qi is proportional to the block difficulty but the reward in Quai is not. Specifically:
- reward_Qi = k_Qi × blockDifficulty_i
- reward_Quai = k_Quai × log2(blockDifficulty_i)
As noted above, log2(blockDifficulty_i) is practically constant, and approximately equals 40.
In the file rewards.go, there are two functions, CalculateQiReward and CalculateQuaiReward. These are called by CalculateReward, which however is only called by a statistics program. More importantly, the two functions are called by NormalizeConversionValueToBlock, which is called by CalculateTokenChoicesSet, which is the voting mechanism and which also updates the counters tokenChoices.Qi and tokenChoices.Quai. CalculateQiReward is also called by the conversion functions QiToQuai and QuaiToQi. QiToQuai and QuaiToQi are called in slice.go by the function Slice, which is the master function that updates the block.
Updating {$k_{Qi}$}
In rewards.go, the function CalculateQiReward divides the block difficulty by the value of the function OneOverKqi located in protocol_params.go. OneOverKqi, as its name implies, calculates the value of {$\frac{1}{k_{Qi}}$} according to a predetermined schedule. The value {$k_{Qi}$} starts at {$\frac{1}{8\times 10^9}$} and then grows linearly for {$2.69$} years until it doubles. Then it grows linearly, at twice that rate, for {$2.69$} years, until it has doubled again. At that point it stays constant at its maximum value, which is {$4$} times its initial value. This growth is meant to signify that the same amount of electricity will yield an increasing amount of computation, at least until 2030. For our purposes, what matters is that {$k_{Qi}$} is predetermined.
Updating {$k_{Quai}$}
The dynamics of the Qi Quai system is captured by the value {$k_{Quai}$}. This is how the controller balances the demand for Qi and Quai.
There is a voting mechanism to determine whether Qi or Quai is more popular. If Qi is more popular, then the controller will increase {$k_{Quai}$} to make Quai more attractive. If Quai is more popular, then the controller will decrease {$k_{Quai}$} to make Qi more attractive. The actual size of the adjustment will depend on the penalty (the "discount") imposed on conversions from Quai to Qi (when Qi per Quai is increasing) and from Qi to Quai (when Quai per Qi is increasing).
The relevant records to consider are in the table newInboundExts (where exts stands for external transactions). This happens in the Slice function in slice.go. This function has to loop through all of these transactions to check which are conversions, and among them, which will incur a penalty, and whether that penalty has been agreed to in advance (as specified in the allowed "slippage"). If the penalty is greater than the slippage, then the transaction will not proceed. Thus the function first loops through to determine which conversions will proceed. In this first loop, it calculates the actualConversionAmountInQuai = a, which is the sum of those conversions that will proceed, where each conversion is valued in terms of Quai. Then, in the second loop, it proceeds with the authorized conversions and imposes any penalties.
The penalties are meant to discourage converting Quai to Qi, in the event that the value of Qi per Quai is increasing, and converting Qi to Quai, in the event that the value of Quai per Qi is increasing. These penalties are known as the K-Quai Discount and the Cubic Conversion Flow Discount. I did not analyze their details because they are rather far removed from the basic dynamics.
The sum of the conversions, after penalties, is the realizedConversionAmountInQuai = r. The actual penalty (known as the "discount") {$P = 1 - \frac{r}{a}$} is the percentage lost in the conversion, which has a maximum of {$90%$}, but regardless, is less than the authorized slippage.
The size of the penalty will determine the size of the adjustment in the block difficulty. But the sign of the adjustment, whether {$k_{Quai}$} will increase (+) or decrease (-), is determined by a voting mechanism in rewards.go. This mechanism considers both conversions and miner choices to determine which is more popular, Qi or Quai. The way this comes together is unavoidably a bit idiosyncratic. The votes are tallied in tokenChoices.Qi and tokenChoices.Quai. A successful miner gets one vote for their choice. But, as often happens, if the miner has split up their choice into different transactions, then each of them gets a vote. Each conversion is converted to block-reward equivalents, discarding the remainder, and it contributes one vote for each block-reward equivalent. Thus if 5.3 block rewards worth of Quai are converted to Qi, then Qi receives 5 votes. But if 0.7 block rewards worth are converted, then they contribute 0 votes. The sum of the votes determines whether Qi is more popular, in which case the sign will be "+" and {$k_{Quai}$} will be increased, or Quai is more popular, in which case the sign will be "-" and {$k_{Quai}$} will be decreased.
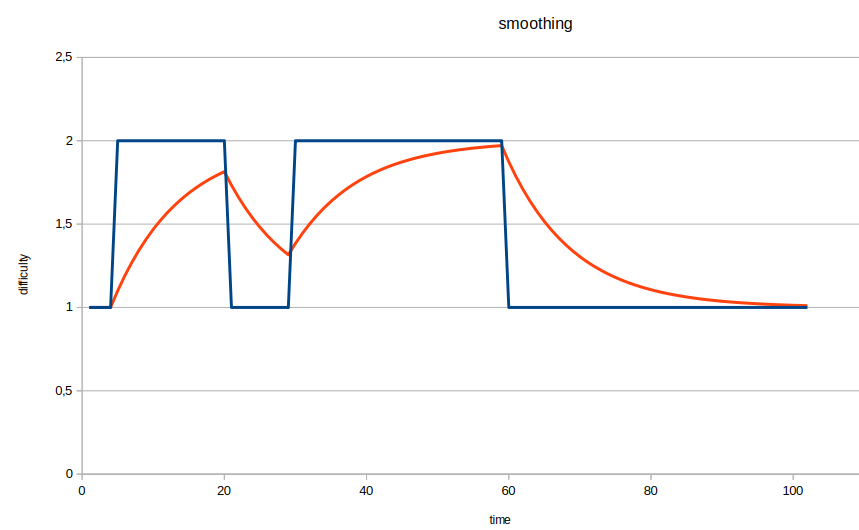
The idea now is to update {$k_{Quai}$} by comparing the actual block difficulty with the "adjusted" block difficulty. But first the block difficulty is smoothed out over the last 4,000 blocks to give what is known as the miner difficulty. This smoothing is done by the Exponential Moving Average over the 4,000 block window. This smoothing is illustrated by the diagram below where the blue curve is smoothed over a 10 block window to yield the red curve. The way that the smoothing proceeds, 90% of the previous value is combined with 10% of the current value, which means that the previous value maintains its influence far beyond the window.
In exchange_controller.go, the miner difficulty is used by the function CalculateTokenChoicesSet to calculate the adjusted difficulty {$A = m[1\pm\frac{1}{5}P]$}. The plus or minus sign was determined by the voting mechanism described above. It's not clear why the number 5=params.TokenDiffAlpha was chosen here but it reduces the impact of the penalty.
This adjusted difficulty is smoothed out over a 4,000 block window to give {$\beta_0$}. Both the miner difficulty and the target difficulty are "normalized" by dividing by their respective logarithms. In the case of the miner difficulty {$m$}, the quantity {$\frac{m}{\log_2 m}$} is called the normalized difficulty. Whereas the {$\frac{\beta_0}{\log_2 \beta_0}$} is called the target difficulty and is calculated in exchange_controller.go by the function CalculateBetaFromMiningChoiceAndConversions. The ratio of the normalized difficulty and the target difficulty determines the nature of the change in {$k_{Quai}$}. Basically, if Qi is more popular than Quai, then the adjusted difficulty is greater than the miner difficulty, then the target difficulty is greater than the normalized difficulty, and {$k_{Quai}$} will be increased. And otherwise, {$k_{Quai}$} will be decreased.
This increase or decrease is damped down by a factor {$\alpha=\frac{1}{1,000}$}. However, if Qi is more popular than Quai, then the increase is further increased by a factor of 3. It's not clear why 3 was chosen. The updated exchange rate is calculated by the function CalculateKQuai in exchange_controller.go.
We can rewrite the update formula in terms of the penalty {$P$} so that the miner difficulty divides away. However, the logarithms do not divide away, which makes for a small multiplicative correction. When {$P$} is small, then the correction can be further simplified by the approximation {$\log_2 1\pm x \approx \pm \log_2 x$}. Of course, we have to keep in mind that first the block difficulty and then the adjusted difficulty got smoothed out over thousands of blocks, and so the subsequent formulas can't be exact but are more for a general understanding.
The upshot is that we can see what factors are most significant in updating {$k_{Quai}$}. We can reduce it to the following simplified mechanism.
Miners who choose Qi receive a reward based on {$k_{Qi}$} that is set ahead of time.
Miners who choose Quai receive a reward based on {$k_{Quai}$} that depends on the history of the popularity of Qi and Quai. Most of the complicated derivation is not actually relevant for this dynamics. Dividing by the logarithm is not relevant, as discussed above. Structurally, the main difference which may stack the relationship in favor of Quai is the multiplicative factor {$S$}. When Qi is popular, then {$S=3$} to make Quai that much more attractive. Whereas when Quai is popular, {$S=1$} and is not a factor.
Otherwise, {$k_{Quai}$} is free to adjust itself up or down based on the relative popularity of Qi and Quai.
As I mentioned above, I have now learned how to correctly calculate Qi rewards (which are denominated in qits) and Quai rewards (which are denominated in Quai). I see that they are roughly equal in value in terms of dollars. This indicates that the control mechanism works.
Now it would be meaningful to get historical data. Then it would make sense to do some numerical simulations of the simplified mechanism to see how that can replicate the historical data. That simplified mechanism can then be made more sophisticated, perhaps by including {$S$}, to see if that adds insight into the behavior.
Then it is sensible to consider this system from a game theory point of view. When does it make sense for miners to choose Qi or Quai? When does it make sense to mine or not mine at all? This is the economic point of view.
Miners will want to mine Quai when the difficulty is lower than it should be. However, the protocol increases the reward for Quai precisely when difficulty is low. This suggests that the controller will not function, will not balance. And yet perhaps it is functioning. This is the kind of question to explore.
The rewards for Qi and Quai are based on very different mechanisms. The reward for Qi is based directly on the difficulty. The reward for Quai is based on the popularity of Qi over Quai. In the next section, I will relate Qi with belief in the system and Quai with belief in belief in the system.
An understanding of the basic dynamics of the preferences of currency miners and currency users can lead us to a conceptually relevant analytic framework such as thermodynamics, Active Inference or experimental psychology.
Investigating the Future of Dual Currency Systems
The Merit of Two or Three Currencies
Bitcoin and other cryptocurrencies are helping us imagine a global economy which is not based on national fiat currencies. They are also helping us appreciate some of the obstacles. One problem with Bitcoin is that it is priced in terms of dollars. This suggests the need for a second currency.
The Qi Quai cryptocurrency system is a response to this challenge. It issues Qi, which serves as a measure of value, and also Quai, which serves as a store of value. It thereby relates these two functions of money. Qi is related to the cost of electricity, which is to say, the cost of energy. Furthermore, "proof of work", by which miners earn coins, can be understood as a search for minimal entropy. Energy, entropy and free energy are fundamental concepts in thermodynamics and also information theory, and specifically, in Active Inference, a theoretical framework centered on the Free Energy Principle.
Steph, thus you asked me to help you investigate how the concepts of energy, entropy and free energy may help us make sense of the Qi Quai cryptocurrency system. I have considered above the Qi Quai system in particular, and now I consider more generally, how these concepts may have meaning for a multiple currency system. I will start by considering economics generally in terms of the functions of money, then learning from the history of Bitcoin about the economy of maintenance, and finally considering the equation that expresses energy in terms of free energy and entropy, representing useful work in disequilibrium and useless work in equilibrium, respectively.
Epistemology of Economics: Four Functions of Money
An enlightening way of approaching economics is to systematize the ways that economists figure things out. Marcus Petz and I collected such ways and I sketched out the system above.
In economics, the entry point is the justification of ownership, which may be profound or ridiculous, but gives meaning to economics. Next, an economic system presumes an underlying dialogue between direct use value (leading to a theory of stewardship) and indirect exchange value (leading to a theory of markets). This dialogue is woven together by a perverse learning cycle, whereby a theoretician elaborates the basis for value, then a party implements those values as policy, and then a school of thought dominates the discourse regarding those values. This leads to the central method, which is to idealize the participant, characterizing their motivation, self-interest, rationality, etc. of the ideal owner.
At this point, we can analyze an economic system in terms of our understanding of this ideal owner, specifically, whether, what, how, why the value of their belongings is maintained. This grounds distinct functions of money.
- Economists imagine how reality may upend expectations, which is to say, whether value is maintained. We may live to see a "black swan" or simply the collapse of the economy as we know it, our world as we know it. Thus an owner wants assurance that their treasure will not be eaten by moths or stolen by thieves. This gives meaning to a store of value.
- Economists understand an economy by making simple models of how authority flows within it, and thus what form the value manifests or maintains. There needs to be a way to show who has the value and thus the authority. This flashy side of value is a function of value (and of money) which has not been recognized but is evident from the epistemology of economics. This gives meaning to money as a focus of authority.
- Economists and investors forecast how economic trends unfold, how value is or can be maintained. They need value to have a mathematical form. This explains money as a unit of account for value.
- In understanding an economic system, economists tease out these three functions of value, which owners convert between, which is why value is maintained. This is the fourth function of value, and the defining function of money, which is a medium of exchange, but primarily exchange between these various forms of value, these various functions of money.
I claim that furthermore there are six methods which economists apply which have them relate pairs of these four functions. The final method of economics is the fostering of a vision whereby an economy grows inclusively, although this leads us out of existing economics, which starts by justifying existing ownership.
This sketch may inspire a collaborative and definitive investigation of the ways that economists figure things out which would clarify what are the ways and how they fit within a system. Its relevance for cryptocurrency is that it provides grounds for characterizing and relating the functions of money.
The distinction between a store of value (Quai) and a unit of account (Qi) is profound. We can wonder whether a cryptocurrency can withstand the collapse of an economy, and in particular, a solar flare that could potentially wipe out the world's computers and its finances along with them. However, the huge investments that have been made in cryptocurrency explain why they retain their value, inasmuch as they do.
The analysis above notes that there is a third function - money as a focus of authority - which an economic system should recognize and include. This points to a weakness in cryptocurrencies. By design, they are decentralized, rather anonymous and typically with protocols (on printing money) that are set in stone. In a sense, this means that authority belonged to the founders but subsequently there is no living authority, there is no governance.
Is nongovernance the best governance? We may witness the collapse of the national economic systems as governments and citizens take on unbearable degrees of debt. And yet there may be better forms of governance and discovering them may be key to founding better economic systems. Economists think in terms of models which show how authority flows in a system, and such models assist in appreciating the system and governing it accordingly.
The economics of maintenance: The cost of doing business
Learning from Bitcoin
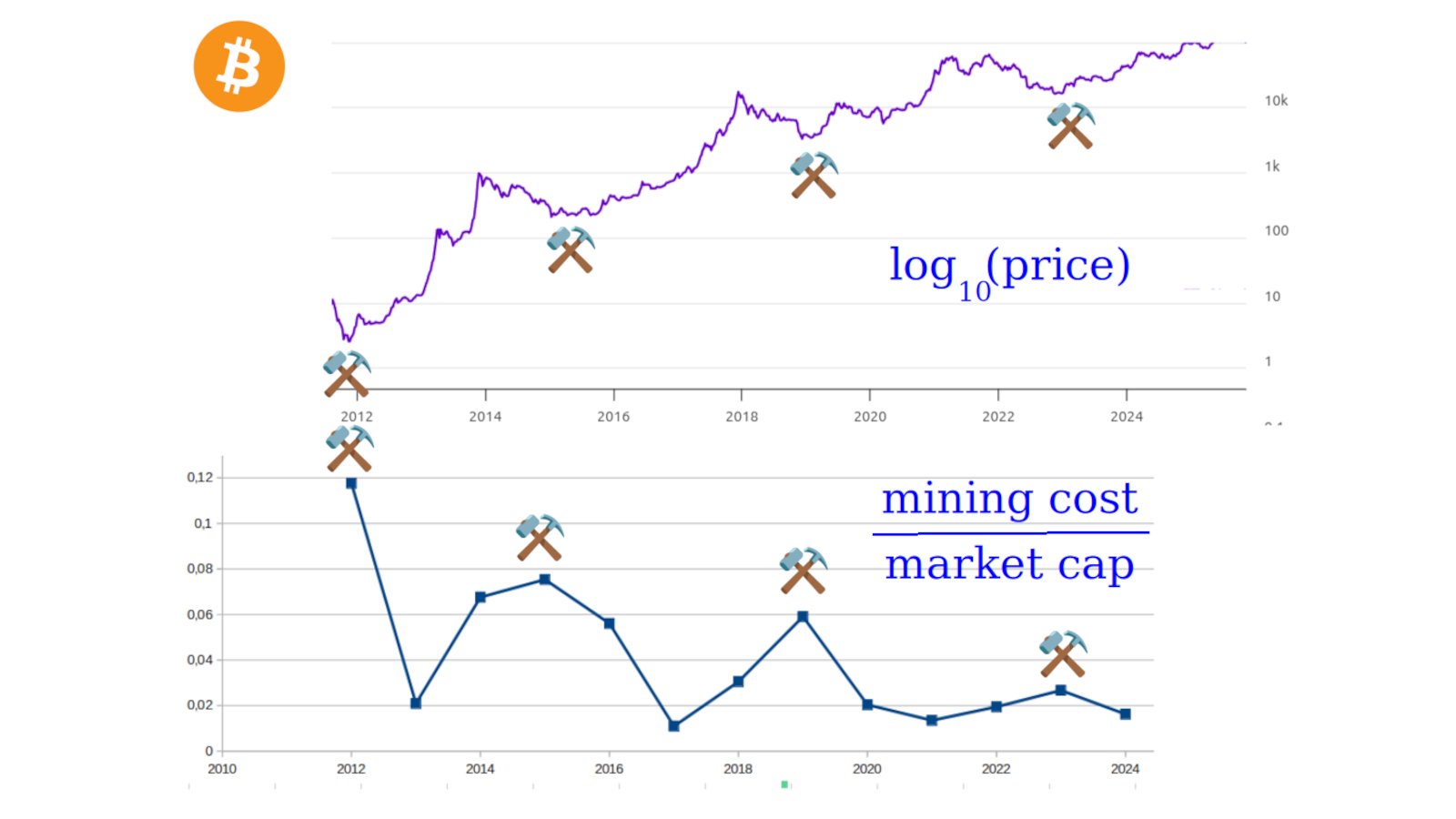
Bitcoin's significance is evident from its market capitalization (roughly 2 trillion USD) and the electricity expended to mine it (rougly 20 billion USD per year). These two numbers reflect the upside and the downside of Bitcoin for humanity. Their proportional relationship can be understood as "the cost of doing business" for the Bitcoin economy, by which I mean, the maintenance expenses required to simply keep things as they are. As noted in the introduction, we can compare this with the cost of doing business for our current economic system. This leads to thinking about an economy of maintenance, in general, and specifically, the maintenance of a civilization or an economy.
Let us consider the data below for Bitcoin, which is available from these sources:
- Bitcoin hashrate historical chart
- Total Bitcoin market capitalization
- Cambridge Bitcoin Electricity Consumption Index
- US electricity prices 2015-2024
| year | tW-hr per year | bitcoins created per year | mW-hr per bitcoin | exa-hash per year | hash per W-hr | US electricity $ per kW-hr | market cap billion $ | $ billion cost per year | energy cost over cap | tera-hash per block |
| 2011 | 0.14 | 2,628,000 | 0.05 | {$1.4 \times 10^{2}$} | {$1.0 \times 10^{9}$} | 0,10 | 0,02 | 0.014 | 90% | 0.0000005 |
| 2012 | 0.10 | 2,505,934 | 0.04 | {$5.2 \times 10^{2}$} | {$5.2 \times 10^{9}$} | 0,10 | 0,09 | 0.01 | 12% | 0.000002 |
| 2013 | 1.06 | 1,314,000 | 0.8 | {$1.6 \times 10^{5}$} | {$1.5 \times 10^{11}$} | 0,10 | 5 | 0.11 | 2% | 0.007 |
| 2014 | 4.73 | 1,314,000 | 4 | {$5.2 \times 10^{6}$} | {$1.1 \times 10^{12}$} | 0,10 | 7 | 0.47 | 7% | 0.02 |
| 2015 | 3.62 | 1,314,000 | 3 | {$1.7 \times 10^{7}$} | {$4.6 \times 10^{12}$} | 0,10 | 5 | 0.38 | 8% | 0.07 |
| 2016 | 5.73 | 998,066 | 6 | {$5.4 \times 10^{7}$} | {$9.5 \times 10^{12}$} | 0,10 | 11 | 0.59 | 6% | 0.2 |
| 2017 | 12.93 | 657,000 | 20 | {$3.0 \times 10^{8}$} | {$2.3 \times 10^{13}$} | 0,10 | 124 | 1.36 | 1% | 1 |
| 2018 | 43.32 | 657,000 | 66 | {$9.3 \times 10^{8}$} | {$2.2 \times 10^{13}$} | 0,11 | 150 | 4.56 | 3% | 4 |
| 2019 | 54.63 | 657,000 | 83 | {$2.3 \times 10^{9}$} | {$4.3 \times 10^{13}$} | 0,11 | 98 | 5.75 | 6% | 10 |
| 2020 | 67.14 | 446,078 | 151 | {$3.8 \times 10^{9}$} | {$5.6 \times 10^{13}$} | 0,11 | 350 | 7.11 | 2% | 16 |
| 2021 | 89.00 | 328,500 | 271 | {$4.6 \times 10^{9}$} | {$5.2 \times 10^{13}$} | 0,11 | 732 | 9.88 | 1% | 22 |
| 2022 | 95.53 | 328,500 | 291 | {$7.1 \times 10^{9}$} | {$7.4 \times 10^{13}$} | 0,12 | 608 | 11.8 | 2% | 30 |
| 2023 | 121.13 | 328,500 | 369 | {$1.4 \times 10^{10}$} | {$1.1 \times 10^{14}$} | 0,13 | 576 | 15.4 | 3% | 54 |
| 2024 | 168 | 216,677 | 775 | {$2.3 \times 10^{10}$} | {$1.4 \times 10^{14}$} | 0,13 | 1,346 | 21.8 | 2% | 91 |
In particular, we can calculate and graph the ratio of mining cost per year over market capitalization, as in the lower graph. And we can compare that with the price of Bitcoin, as in the upper graph, which is logarithmic. Then we see that, in the upper graph, the dips in price, which are quite pronounced, coincide in the lower graph with a high "cost of doing business". Counterintuitively, a low ratio indicates overpricing, whereas a high ratio indicates underpricing. Evidently, a low ratio means that too much value is being attributed to Bitcoin. A high ratio means that a low value is attributed to Bitcoin, the difficulty of mining goes down, and mining is attractive to miners who believe in the future of the system, not just the system as it is at the time. A high ratio indicates that those miners exist.
This ratio is one that should be investigated further, empirically and conceptually. Empirically, we can compare the total value and the annual costs for
- Mining gold, silver, and other mineral production
- Maintaining a house
- Maintaining a road
- Maintaining a car
These examples are different and yet they may share an underlying logic. Thus much gold is held in reserve, unused, but then why is more gold being mined? The fact that gold is "valuable" relentlessly drives further mining even though there is so much gold that is "unused". This mining can be interpreted as the cost of doing business, as regards gold.
Again, counterintuitively, a new car, which requires little maintenance, is evidently overpriced. Whereas an old car that requires significant maintenance is, on average, underpriced. This may seem a wrong headed way to think but, rationally speaking, it may actually be correct.
In economics, a distinction is made between fixed costs and variable costs. A company invests in a factory, which is a fixed cost that does not depend on how much the factory is actually used. It also pays variable costs, such as wages, which relate to the actual production. The company can cease production and let go of the workers. However, for a civilization, there is no humane way of letting go of its people, although there are options such as war. Generally, a civilization faces many fixed costs, namely keeping its people alive, fed, clothed, sheltered, and more generally, keeping certain basic functions going, which can include communications systems, transportation systems, internal and external security, and a government bureaucracy, also known as administration. If a civilization fails to pay these fixed costs, then it collapses.
The fixed costs of a civilization may further include providing for various presumed obligations, which keep people aligned, such as realizing the American dream of home ownership, or assuring an exponentially improving lifestyle, or sustaining an ideological fervor, or imposing a state police and a regime of terror. In my understanding, after Stalin's death, the Soviet Union switched from imposing a regime of terror to providing a rudimentary consumer lifestyle. So long as people's lives improved exponentially, they stayed in line, despite Western competition. But ultimately even the vast mineral resources were not enough to sustain such growth. The Soviet Union collapsed. I think it was because it could not meet the basic consumer expectation of ever improving standards of living.
The relation between the total value of the system and the annual cost of maintaining it suggests two distinct points of view, the game players who believe in the system, and the game makers who believe in the belief in the system.
When an economic system is founded, as with cryptocurrency, then at first there are no economic transactions. There is no system to believe in! However, the organizers and miners believe in that belief, they believe that there will be believers. And so they invest themselves in organizing and mining. At a certain point, some of those miners may lose faith and yet they do have coins. Those coins have value in the eyes of those who continue to mine. And so those coins can be exchanged for cash or for goods. Or those coins may be retained and used with the understanding that there will be ways to redeem them. This is a scenario by which there arise game players, those who believe that the currency has some value, and thus can serve some function. In that sense, they believe in the system, but they do not have a greater belief by which they would invest themselves in that system, in maintaining it and profiting from it.
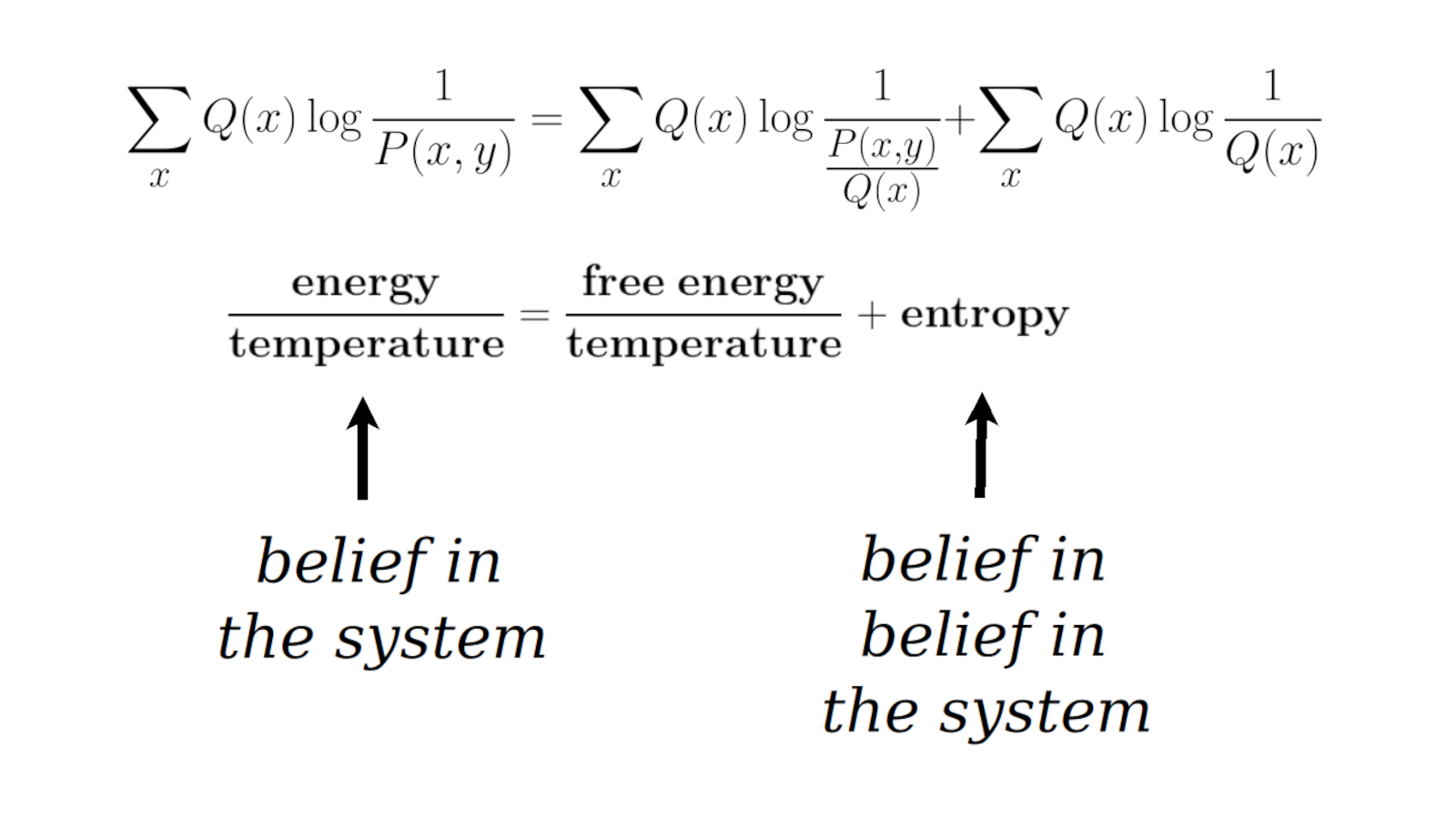
I think this can be a helpful and fruitful distinction. First order, direct, sensory belief in a system, and second order, indirect, conceptual belief in belief in a system, brings to mind the dialogue between direct use value and indirect exchange value. In myriad ways, a similar dialogue manifests itself between levels of awareness, namely an unconscious sensory mind that knows answers, and a conscious conceptual mind that does not know directly, thus asks questions. At Theory Translator, we're collecting many such examples. Importantly, we can consider a dialogue between two probability distributions, {$P(x,y)$} and {$Q(x)$}, which leads us to the subject of energy, entropy and free energy.
Theory Translator includes examples of a third and final level of awareness, which is belief in belief in belief in the system. This third mind is an investigating mind which considers the greater purpose of the economic system, how the game players and game makers need each other and can benefit from each other. The third mind offers the vantage point for governance, when to think in terms of the game players and when to think in terms of the game makers.
Thermodynamics: Energy, entropy, free energy
In trying to understand currency systems, we have distinguished two points of view: the game players who believe in a system and the game makers who believe in that belief in the system. Mathematically, we can now search for this distinction in thermodynamics, and specifically, in the formula that expresses energy in terms of free energy and entropy. I will interpret this formula as a dialogue between two probability distributions, {$P(x,y)$} and {$Q(x)$}.
In physics or chemistry, this formula is written as {$U = F + TS$} or {$\frac{U}{T} = \frac{F}{T} + S$} where {$U$} is the internal energy of the system, {$T$} is temperature, {$S$} is entropy and {$F$} is the Helmholtz free energy (which is the available energy for doing work).
In the Active Inference textbook by Parr, Pezzulo, Friston, 2022, the formula takes the form {$F[Q,y]=-\mathbb{E}_Q(x)[\ln P(x,y)] - H[Q(x)]$}, as equation 2.5, where the free energy, on the left hand side, equals energy minus entropy, on the right hand side. Here {$\mathbb{E}_Q(x)$} indicates the expected value with regard to the weight {$Q(x)$}. The formula is often written using the Kullback-Leibler divergence, known as the KL-divergence: {$D_{KL}|Q(x)\parallel P(x,y)| = \sum_x Q(x)\ln \frac{Q(x)}{P(x,y)}$}. For me, the left hand side is statistical jargon, so I prefer the right hand side, which I find understandable.
As regards notation, the natural logarithm {$\ln = \log_e$} is the logarithm with respect to base {$e=2.718...$}. In writing {$\log$}, I am not specifying the base but it may be {$2$} or {$e$}, as appropriate. Generally, in physics it is {$e$} but in information theory it is {$2$} when we are measuring information in binary choices, bits.
In what follows, I provide my own interpretation of this formula as a dialogue between {$P(x,y)$} and {$Q(x)$}. I interpret the entropy term and then the energy term.
Entropy is a word for a mysterious concept that is equated with vaguer concepts such as disorder and randomness. But mathematically entropy is a precise concept that means ambiguity, the number of configurations that satisfy given constraints. Entropy supposes that there are two frames, a coarse frame that defines the constraints on a system (such as its overall volume, pressure, temperature) and a refined frame that specifies the configurations (such as the position and momentum of each particle).
Entropy is a property of a probability distribution. If the probability distribution is {$Q(x)$}, then its entropy is typically written as {$-\sum_x Q(x)\log Q(x)$}. Note that {$Q(x)$} appears twice in the formula. This means that it is playing two different roles, which I will separate out.
Consider {$-\log Q(x)=\log Q(x)^{-1}=\log \frac{1}{Q(x)}$}. The right hand side is more informative than the left hand side, which is why I write it out this way. Since {$Q(x)$} is a probability distribution, we know that {$0\leq Q(x)\leq 1$}. Assuming that {$Q(x)\neq 0$}, we have that {$\frac{1}{Q(x)}\geq 1$} and thus {$\log \frac{1}{Q(x)}\geq 0$} is positive or zero. So I prefer writing it like this rather than {$-\log Q(x)$} where I find the negative sign confusing because the value is not negative. Here I also note that, in the right hand side, we cannot have {$Q(x)=0$}, and so from this perspective, states {$x$} with zero probability do not exist. Whereas from the perspective of {$-\log Q(x)$} there can be states {$x$} with zero probability but they contribute zero entropy. This is a philosophical distinction to keep in mind.
The quantity {$\log \frac{1}{Q(x)}$} is the knowledge gained, also known as information gained or surprise. For example, if we flip a coin three times, then there is one-eight chance that it will fall heads-tail-heads, for example. The number {$\log_2 \frac{1}{\frac{1}{8}}=\log_2 8 = \log_2 2^3 = 3$} indicates that the knowledge gained is {$3$} bits, thus {$3$} binary choices, yes or no.
The expression {$\sum_x Q(x)$} is the expected value with regard to the weight {$Q(x)$}. We can think of this as the knowledge lens, the way things look from a particular perspective. For example, we can take the Earth's perspective, and consider states "land" and "ocean", where {$Q(\textrm{land})=\frac{1}{4}$} and {$Q(\textrm{ocean})=\frac{3}{4}$}. We can then weight any function accordingly to get its expected value.
Entropy is the weighted value of the knowledge gained. In the case of the land and the ocean, the land is less likely {$\frac{1}{4}$} but the knowledge gained is larger, {$\log_2 \frac{1}{\frac{1}{4}} = \log_2 4 = \log_2 2^2 = 2$}, whereas the ocean is more likely {$\frac{3}{4}$} but the knowledge gained is less, {$\log_2 \frac{1}{\frac{3}{4}} = \log_2 \frac{4}{3} \approx \frac{2}{5}$}. Thus the land contributes more entropy {$\frac{1}{4}\times 2 = \frac{1}{2}$} than the ocean {$\frac{3}{4}\times \frac{2}{5} = \frac{3}{10}$}. The land contributes more ambiguity, more uncertainty than the ocean. The ocean contributes more certainty, for example, as regards to where an asteroid would fall on Earth.
Entropy is defined in terms of probability. But probability supposes an event, a selection. Before the selection, there are multiple choices, there is ambiguity. But after the selection there is only one choice that was made. Thus we need to be careful if our perspective is before the selection, when there is uncertainty, or after the selection, when there is certainty.
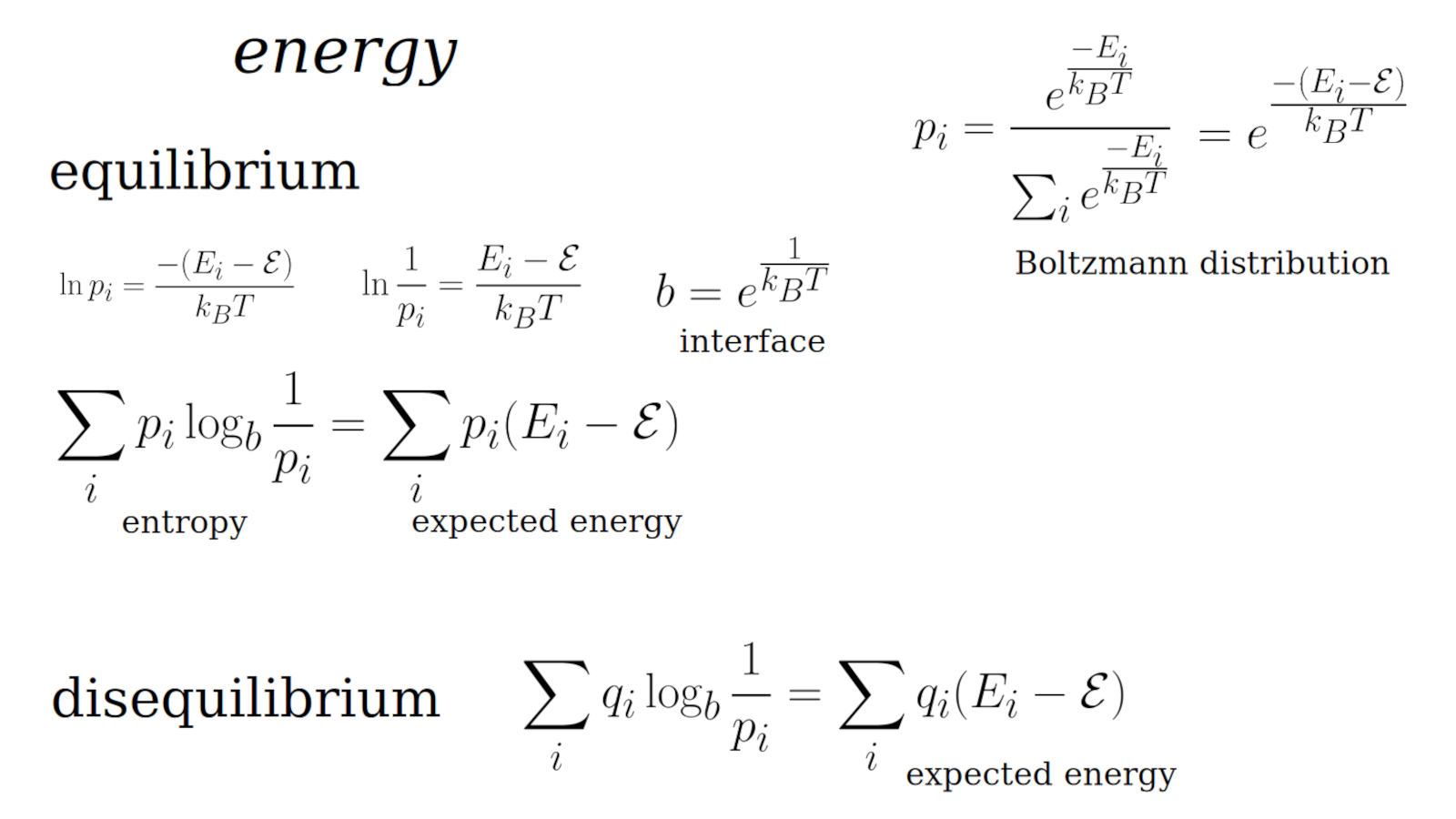
Let us now consider energy. The Boltzmann distribution describes the probability {$p_i$} that a system will be in a state {$i$} with energy {$E_i$}. This holds when a closed system is in thermal equilibrium.
The probability {$p_i$} has a denominator {$Z=\sum_i e^\frac{-E_i}{k_BT}$} which sums over all of the states and thereby ensures that the probabilities add up to 100%, {$\sum_i p_i=1$}. {$Z$} is known as the canonical partition function and {$k_B$} is Boltzmann's constant which is specific to the physics of gases.
Instead of writing the constant {$Z$} as a denominator, we can define a base level energy {$\mathcal{E}$} such that {$Z=e^\frac{-\mathcal{E}}{k_BT}$}. This way, in place of {$Z$}, we can incorporate {$e^\frac{-\mathcal{E}}{k_BT}$} seemlessly into the formula for {$p_i$} so that it calibrates the energy level {$E_i$} with regard to {$\mathcal{E}$}, giving {$E_i-\mathcal{E}$}.
Then we can calculate the knowledge gained {$\ln \frac{1}{p_i}=\frac{E_i-\mathcal{E}}{k_B T}$}. We see that it is just the energy times a constant {$\frac{1}{k_B T}$}. We can absorb this constant into the base of the logarithm by writing {$b=e^{\frac{1}{k_B T}}$} whereby {$k_B T\ln\frac{1}{p_i}=\log_b \frac{1}{p_i}$}. In this simplification, we are using the fact that if {$c\ln a = \log_b a$} then {$b^{c\ln a}=a$}, {$\ln b^{c\ln a}=\ln a$}, {$c\ln a \ln b=\ln a$}, {$c \ln b=1$}, {$\ln b=\frac{1}{c}$} and so {$b=e^{\frac{1}{c}}$}. We apply this to our case where {$a=\frac{1}{p_i}$} and {$c=k_BT$}. Note that the temperature {$T$} gets absorbed into the base of the logarithm.
This gives us the energy {$E_i-\mathcal{E}=\log_b\frac{1}{p_i}$} for a particular state {$i$}. But energy, in physics, means "the expected value of energy". Thus we write {$E=\sum_i p_i\log_b\frac{1}{p_i}$} where we are summing over all of the states {$i$} and weighting accordingly. But this is the formula for entropy! How is it that energy equals entropy? Recall that the Boltzmann distribution applies when the system is at equilibrium, which is when no useful work can be done. Thus there is no free energy in this situation. The energy is simply the entropy.
We thus see what it means to get the formula we had for entropy. We have to separate the knowledge lens {$Q(x)$} and the knowledge gained {$P(x,y)$} so that they are two different distributions. There needs to be a disequilibrium, a difference between the knowledge we are gaining (from the world) and the knowledge lens we are applying (how we ourselves look at that world).
This helps us see that entropy is a degenerate form of energy. Entropy is the special case when the knowledge lens and the knowledge gained are given by the same distribution.
Energy is the general case where they are different, and this is also known as cross-entropy. It can be interpreted as the expected message-length per datum when a wrong distribution {$q$} is assumed (for the knowledge gained) while the data actually follows a distribution {$p$} for the knowledge lens.
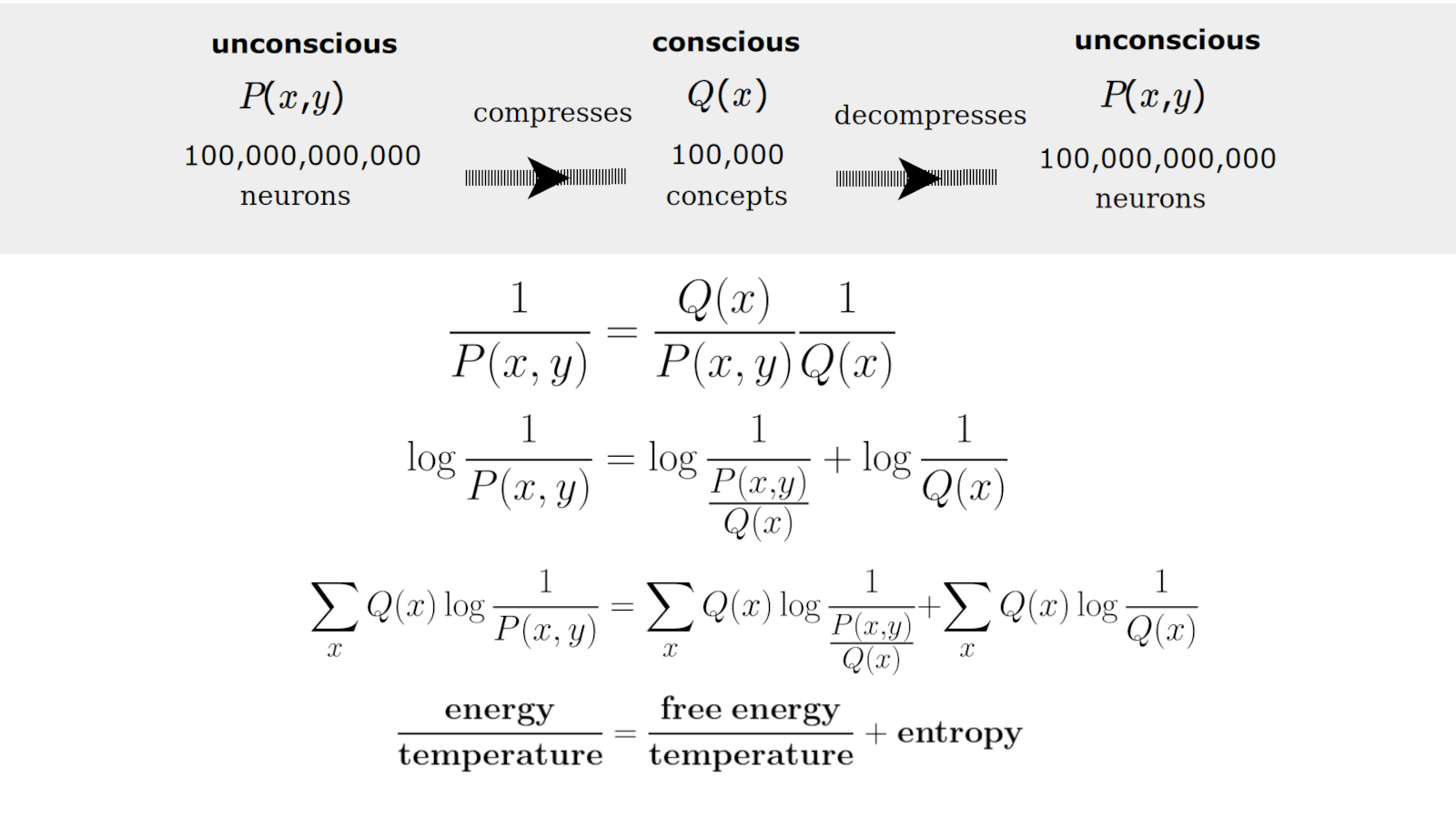
We can now derive and interpret the formula as a dialogue between two probability distributions {$P(x,y)$} and {$Q(x)$}. Specifically, we can consider {$y$} to be as evidence in the world, such as a shadow, and we can consider {$x$} to be an inferred cause, such as a hand. The distribution {$Q(x)$} only sees the cause {$x$} whereas the distribution {$P(x,y)$} sees both the evidence {$y$} and the cause {$x$}. To make this all concrete, we can think of {$P(x,y)$} as the sensory information provided by 100 billion neurons in the human brain, which includes sensory information such as a visual image of a shadow but also a proprioceptor that indicates one's hand is moving. We can think of {$Q(x)$} as a compression of {$P(x,y)$} so that basically the same information is given by 100 thousand concepts or words or black boxes or cortical columns in the brain. But {$Q(x)$} does not consider the external evidence but simply thinks in terms of a vocabulary of actions, causes, conceptualizations. More generally, we can think of {$P(x,y)$} and {$Q(x)$} as two different levels of awareness, two different kinds of minds. {$P(x,y)$} is a mind that unconsciously knows answers and {$Q(x)$} is a mind that consciously does not know, thus asks questions.
Mathematically, we can use {$Q(x)$} to break up {$P(x,y)$} into what is useful and useless from the perspective of {$Q(x)$}. Starting with the equation {$P(x,y)=P(x,y)$} we simply multiply and divide the right hand side by {$Q(x)$}, yielding {$P(x,y)=\frac{P(x,y)}{Q(x)}Q(x)$}. We can flip this upside down {$\frac{1}{P(x,y)}=\frac{1}{\frac{P(x,y)}{Q(x)}}\frac{1}{Q(x)}$}. This is multiplicative and we can make it additive by applying logarithms. And then we can take the expected value with regard to {$Q(x)$}. This gives us the desired formula.
The formula breaks up energy into free energy and entropy. In all three terms, the knowledge lens is given by {$Q(x)$}. In all three terms, the knowledge gained is different. For energy, the knowledge gained is given by {$P(x,y)$}. For free energy, it is given by {$\frac{P(x,y)}{Q(x)}$}, which can be thought of as {$P(x,y)$} from the view of {$Q(x)$}. For entropy, it is given by {$Q(x)$}. Thus we see that the useless work, entropy, is that where the knowledge lens and the knowledge gained are given by the same distribution, and so there is no tension. But in free energy we have the useful tension between the knowledge lens {$Q(x)$} and the sensory world from the view of that lens, {$\frac{P(x,y)}{Q(x)}$}. Thus energy is broken down into these two terms. The two terms depend on {$Q(x)$}. Given {$P(x,y)$}, if we want there to be useful work, we need a tension between {$P(x,y)$} and {$Q(x)$}, but then there will also have to be useless work relating {$Q(x)$} with itself. That is the intuition that the math is expressing.
We can apply this interpretation to analyze currency. In setting up a currency system, there will be a useless aspect, the entropy, which is the system's value in its own eyes, "the belief in the belief in the system". There will also be a useful aspect, the free energy, which is the system's value more broadly, with regard to the greater world, "the belief in the system".
As discussed in the introduction, there are different ways to apply this, depending on the knowledge lens we take. If we consider the "cost of doing business" for a civilization, then the useless part is the upkeep, the basic economy needed to just keep it going, and the free energy is expressed by the capital projects that the system makes possible. But if we consider the "cost of doing business" for an economy, then the useless part is the financial infrastructure, and the useful part, the free energy, is all of the personal solutions by which individuals pursue their happiness. Thus we are led to define our perspective, our knowledge lens, and what we are looking at.
This formula for energy could be the starting point for Active Inference and the Free Energy Principle but it is not. In general, the Active Inference framework does not consider entropy but focuses on free energy and how that breaks down.
We can further break down the free energy into divergence and knowledge gained.
This follows straightforwardly from the equation {$P(x,y)=P(x|y)P(y)$} where {$P(y)$} is the probability of the evidence {$y$}, {$P(x|y)$} is the probability of {$x$} given {$y$}, and {$P(x,y)$} is the probability of both {$x$} and {$y$}. Thus free energy breaks down into divergence and surprise.
Free energy can also be broken down into exploration and exploitation, or complexity and accuracy, or ambiguity and risk. I expect that these have similarly simple derivations. But this goes beyond the work I have done so far. Empirically, as regards Qi and Quai, I don't have data to consider, and so conceptually, I don't have a basis for developing such more sophisticated insights in any meaningful way without just making things up.
I have focused on the formula relating energy, free energy and entropy. Active Inference considers a version that relates two probability distributions {$P(x,y)$} and {$Q(x)$} but I have not seen that in the literature for physics or chemistry. So I am curious to learn more about the history of this particular version.
The 2006 paper Karl Friston, James Kilner, Lee Harrison. A free energy principle for the brain., introduced the free energy principle. There the free energy has the form {$F=-\int q(\mathscr{v})\ln\frac{p(\tilde{y},\mathscr{v})}{q(\mathscr{v})}$}, with a continuous integral rather than a discrete sum. This paper cites the 2003 paper Karl Friston. Learning and inference in the brain. which has the same formula and cites the 1976 paper A.P.Dempster, N.M.Laird, D.B.Rubin. Maximum Likelihood from Incomplete Data via the EM Algorithm. This latter paper calculates maximum likelihoods with a two-step algorithm, consisting of an expectation-step and a maximization-step. Equation 2.6 is perhaps a key equation for maximizing {$L(\phi)=\log f(x|\phi)-\log \frac{f(x|\phi)}{g(y|\phi)}$}, which is perhaps minimizing free energy {$-L(\phi)=\log \frac{g(y|\phi)}{f(x|\phi)} + \log \frac{1}{f(x|\phi)}$} as divergence plus knowledge gained. The 2003 paper also cites the work of Geoffrey Hinton. A paper not cited but yet helpful and relevant is Geoffrey E. Hinton, Richard S. Zemel. Autoencoders, Minimum Description Length and Helmholtz Free Energy.
It seems that the EM algorithm showed the significance of the combination of divergence and knowledge gained. Hinton recognized that the quantity which is minimized is the free energy. Friston then developed the Free Energy Principle as a general principle which organisms apply to make the most of that combination. But I would want to consider what this truly means in terms of energy and entropy, the formula that I considered.
I have given an interpretation of the formula for energy, free energy and entropy which is an alternative to the customary interpretation given in the Active Inference framework.
In both interpretations, {$y$} refers to evidence and {$x$} refers to an inferred cause. {$P(x,y)$} has access to {$y$} but {$Q(x)$} does not.
In my interpretation, there is a dialogue between two distributions {$P(x,y)$} and {$Q(x)$}. They are equal and independent participants. {$Q(x)$} is a compression of {$P(x,y)$}. They can be thought of as two levels of awareness or simply two minds. {$P(x,y)$} expresses a sensory mind that unconsciously knows answers (as provided by 100 billion neurons) and {$Q(x)$} expresses a conceptual mind that consciously does not know thus asks questions (as provided by 100 thousand cortical columns) in the form of concepts, words, black boxes, which express actions or conceptualizations. These two distributions express the same information in two very different ways. {$P(x,y)$} is passive, enactive, whereas {$Q(x)$} is active, predictive, and thus they have a meaningful dialogue.
In the customary interpretation, {$Q(x)$} is an approximation of the generative model {$P(x|y)$}, which is predictive. The goal is to calculate the posterior belief {$P(x|y)$}, which is the belief in {$x$} given the evidence {$y$}. This is done using Bayes's theorem {$P(x,y)=P(x|y)P(y)=P(y|x)P(x)$}. Thus we can calculate {$P(x|y)=\frac{P(y|x)P(x)}{P(y)}$}. But it is noted that the probability of the evidence {$P(y)=\sum_x P(y|x)$} is intractable to calculate because it would have to be done over all possible causes {$x$}. Instead, {$Q(x)$} is introduced as an approximation for {$P(x|y)$}. The Free Energy Principle is assumed to apply so that the best approximation is achieved. But free energy is simply used as an upper bound on surprise, the knowledge gained {$\ln \frac{1}{P(y)}$}.
My alternative interpretation has a derivation that is direct and simple. There is no need to appeal to Bayes's theorem. That is because I am not assuming predictive processing. In my alternative interpretation, we freely and carefully construct {$Q(x)$} so that it is a meaningful world of concepts, and we may well do that predicively. And that can interact with the passive, sensory information {$P(x,y)$} about the greater world. But the customary interpretation claims the opposite, that {$P(x,y)$} is the generative model that we construct, whereas {$Q(x)$} is provided automatically by the Free Energy principle.
My alternative interpretation and derivation show that there is no need to think in terms of Markov systems or Markov blankets or perception-action loops. The equation requires only that we distinguish the sensory evidence {$y$} of the greater world from the causes {$x$} that we conceive. The customary interpretation supposes that there is a system of states and a boundary shared by a self and its environment. This raises the problem of whether reality itself is such a conceptualization in terms of states. The alternative interpretation supposes instead that there is a gap between two systems where {$Q(x)$} is conceptualized but {$P(x,y)$} need not be. This raises the problem of how that gap is overcome, how relationships on one side accord with relationships on the other side.
These differences are pronounced in the choice between policies to take. The customary interpretation supposes that policies - sequences of possible actions - are selected based on our preferences for the evidence {$y$} that we wish to see. Which is to say, we choose our actions based on the shadows that we want to see, not the hands that we want to move. I think this can only make sense if we understand this from a historical point of view, where behaviorialist B.F.Skinner critiqued mentalism as fictitious, unscientific folklore. For him, reality was observed external behavior, and so he studied rats in mazes. Predictive approaches suggested subsequently that a rat brain could act as if it had a model. But it was perhaps too bold to say that the model was real. And so instead the preferences were not for the causes but for the evidence. The alternative interpretation would allow that the preferences are not for the evidence, and perhaps not for the causes, but rather for a further compressed distribution R(z), which may perhaps have only 8 contexts in which to evaluate the policies. This further compression into mental contexts (such as "divisions of everything") may serve to align {$P(x,y)$} and {$Q(x)$} contextually.
In the alternative interpretation, the knowledge lens is {$Q(x)$}. But {$Q(x)$} is conceptual, constructed to look at disparate concepts, whereas {$P(x,y)$} is holistic, distilling the whole. It would thus make more sense for {$P(x,y)$} to be the knowledge lens. Then the formula would be {$\sum_x P(x,y)\log\frac{1}{Q(x)}=\sum_x P(x,y)\log \frac{1}{\frac{Q(x)}{P(x,y)}}+ \sum_x P(x,y)\log\frac{1}{P(x,y)}$}. This means that the conceptual mind {$Q(x)$} serves to break up the sensory mind into useful and useless parts. This may be perfectly fine and true. But it diverges markedly from the Active Inference framework. It would need a lot of conceptual grounding, empirical application and practical validation. It would help to have an understanding of the history that led to the current formula.
Related notes